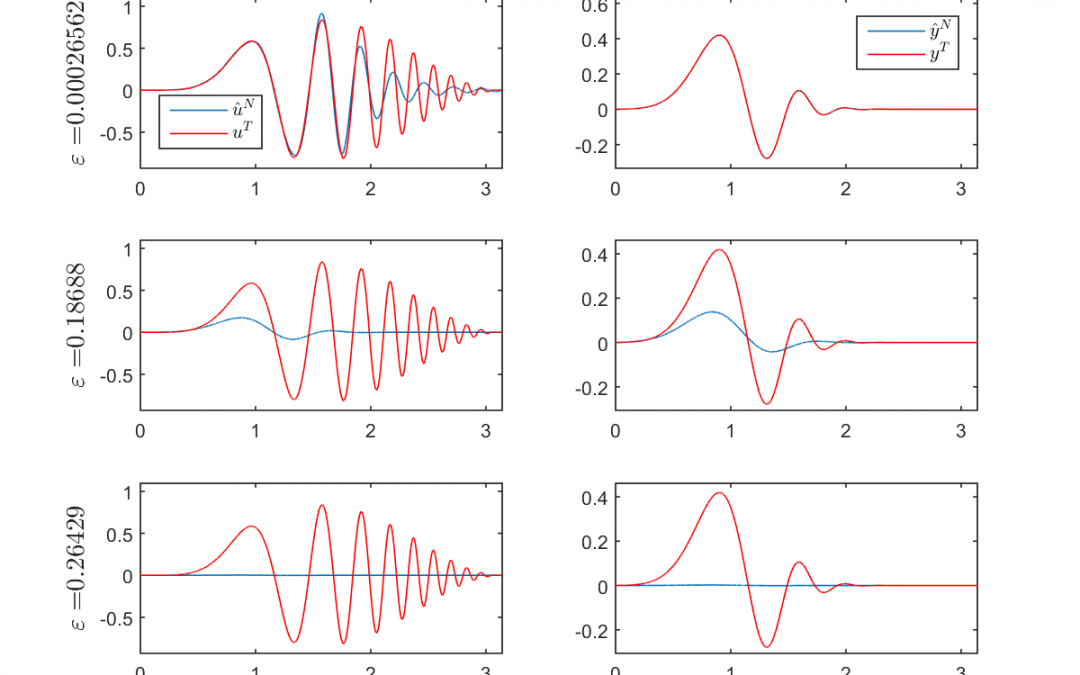
This paper deals with an optimal control problem of Bolza type for a class of parabolic equations. It consists in finding the initial datum that minimises a cost functional, which comprises an energy term on the control and a regulation term given by a distributed cost on the state, and such that the final state lies within a prescribed distance to a given target. Beyond the particularities of the chosen problem, our aim here is to propose a new methodology –?based on a spectral decomposition of the operator governing the evolution of the system–?, describe its implementation for this kind of problem, and finally perform some preliminary numerical experiments to assess its behavior.
Optimal control of parabolic equations by spectral decomposition (PDF Download Available). Available from: https://www.researchgate.net/publication/296678908_Optimal_control_of_parabolic_equations_by_spectral_decomposition
Optimal control of parabolic equations by spectral decomposition
